MAQUINA DE ATWOOD Y SEGUNDA LEY DE NEWTON

	Sign In Sign-Up

MAQUINA DE ATWOOD Y SEGUNDA LEY DE NEWTON

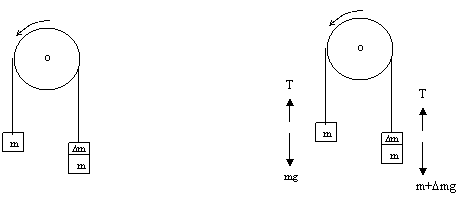
Este arreglo de polea, ayuda a tener una idea cinestética de la segunda ley de Newton al comparar dos sistemas de distinta masa total (polea +100 g, polea +200 g).

Aplicando la segunda ley de Newton a cada carga del sistema se obtienen las siguientes ecuaciones:

Fuerza total al lado izquierdo:

T - mg = ma_i;

como las dos aceleraciones son iguales ya que en el mismo tiempo una masa sube una distancia igual a la que baja la otra masa, a_d = a_i =a.

Fuerza total al lado derecho de la polea:

(m+Dm)g – T = (m+Dm)a_d

mg es el peso de esta masa, a_d es la aceleración de la masa.

Al sumar estas dos ecuaciones entre sí se obtiene:

(m+Dm)g – T = (m+Dm)a_i

T - mg = ma_i

___________________________

(m+Dm)g – mg = (m+Dm)a + ma; las tensiones T, se cancelan al sumar y hemos reemplazado a_i por a.

mg+Dmg – mg = ma+Dma_d + ma

Dmg = (m+m+Dm)a

Dmg = M_ta M_t es la masa total del sistema.

a = D m g/ M_t La aceleración del sistema de masas es entonces:

= [D m/ M_t ]g.

Ejercicios: calcular cuanta fuerza se necesita si se quiere dar a un sistema, la misma aceleración que otro que tiene la mitad de la masa.

Calcular cuanta aceleración debe tener un sistema que tiene el doble de masa que otro, si se imprime la misma fuerza a ambos sistemas.

Ej. 5.5 Halliday/Reskick/Walker. Wiley&Sons.

atwood

Fuerzas verticales: Fuerza sobre el bloque M: F_N (hacia arriba), F_g (su peso hacia abajo)

Fuerza sobre el bloque m: T (hacia arriba), F_g (su peso hacia abajo).

Fuerzas horizontales: Fuerza sobre el bloque M: T (hacia la derecha), m no tiene fuerzas horizontales.

Sobre el bloque M:

F_y: F_N-F_g=Ma_y = M(0) = 0 el bloque no se mueve en la vertical.

F_N =F_g =Mg; significa que el peso de este bloque es igual a la fuerza normal que hace la mesa sobre él.

F_x: T = Ma_x esta es la aceleración que le imprime el bloque m.

Sobre el bloque m:

F_y: T-F_g=ma_y = -max;

T-mg = -max; recordar que esta es la misma aceleración que le imprime al bloque M.

Al combinar estas dos ecuaciones (color rojo).

a_x = m g/ M_t La aceleración del sistema de masas es entonces:

a_x = m g.

(M+m).

Si se sustituye esta a en la otra ecuación para T, se puede encontrar el valor de la tensión en la cuerda;

T = M m g.

(M+m).

Notar que T=0 si m fuese infinita y M=0.

Referencias:

Benson H.; University Physics, Rev. Edition; John Wiley & Sons, New York, (1996).